4 in a row Tutorial

A Brief Introduction to 4 in a row

4 in a row is a rather simple board game. At least the rules are simple. But how about the game? 4 in a row is solved, i.e. the game has been calculated from start to end by computer and it has been proven that the player to start can always win. However only if she puts the first stone in the central column. For humans, 4 in a row remains a challenge. This tutorial is supposed to give you some ideas on how to play if you want to win. To begin, let me state the obvious - if you want to get four stones in a row, you must first have 3 of your stones in the row (or diagonal). And before you have 3 stones in a 4-row, you must first have 2 there. And before...
figure 1 So the first simple lesson is this: drop your stones in places where they will have the biggest effect in terms of 4-rows in which they participate. This is illustrated in figure 1: denoting squares by columns a through g and rows by 1 through 6, we can see that square a1 which is indicated by the red arrow only participates in 3 4-rows, whereas square d3, indicated by the blue arrow participates in 4 horizontal, 3 vertical and 6 diagonal 4-rows, making a total of 13 4-rows - a stone on d3 is much more effective than one on a1.
If either side does not follow this basic principle, the other side will get lots of tactical possibilities. I am going to refer to forcing winning lines as "tactical", whereas there is also a long-term strategic goal to the game. First, I would like to look at some typical 4 in a row tactics. They usually work by creating two threats to get 4 in a row which can not be stopped simultaneously, or by creating a threat which can still be stopped, but stopping the threat loses in another way.
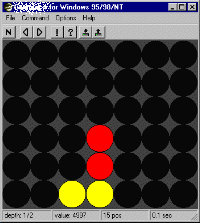
figure 2

Figure 2: Yellow to play and win

Figure 2 shows a very simple win for yellow. He can either play b1 or e1, creating either the threat to get 4 in a row with a1 or e1 or, in the case of e1, to get 4 in a row by playing b1 or f1. Red can obviously not stop both threats at once and loses. Most tactical possibilities are similar to this, but a bit more complicated.
figure 3

Figure 3: Yellow to play and win

Figure 3 also shows a simple win for yellow: by playing e3 he creates the threat f3, forcing red to answer f3, but then yellow plays f4 and gets 4 in a row in the diagonal.
figure 4

Figure 4: Yellow to play and win

Figure 4 shows a more complicated forced win for yellow. By combining immediate threats, he wins: d5 forces red to play d6, then f3 forces red to play f4, and e3 forces red to play g1. Note that a different move order would also work in this example. Now yellow plays e4, leading to figure 5.
figure 5

Figure 5: Red to play

In figure 5 yellow has created a vertical double threat by the forced sequence from figure 4: yellow could win by either taking g2 or g3. Such a constellation always wins immediately (of course only in the absence of direct threats of the other side). Red has to put a stone on g2, but then yellow wins with g3. A vertical double threat wins because the side which owns the threat can just start filling in the column, until he threatens to win with the lower of the two threats, and the other side cannot stop him because stopping the first threat will allow the second one to be executed.
Tactical wins are nice, but usually only possible against inexperienced players. Stronger opponents will never allow you such quick wins. This is the point where strategic considerations become important. The geometry of the board is important here, or, to be more precise, the height of the board is decisive - there are 6 rows. That means that if all but one columns are filled, the side to start - yellow - will end up occupying all squares in the odd rows of the remaining column, while red will end up with the even squares. This simple fact is very important: yellow has to aim for a threat on odd rows, while red has to aim for a threat on even rows. If red has one threat on an odd row, he will not win, and yellow can not win with one threat on an even row. The two sides have to adopt different strategies, then, making 4 in a row an asymmetric game.
figure 6

Figure 6: Yellow to play

We have seen that one threat for yellow on an even row won't win. How about two? This situation is shown in figure 6. Yellow has created two even threats on the second row. However, this also doesn't help him. Once the remaining 5 columns are filled, yellow has to play in column b or f, losing his threat there. He keeps one even threat - which leads to a draw.
figure 7

Figure 7: Yellow to play

Two even threats for yellow don't win - so how about two odd threats for red? In figure 7, red has created two odd threats - and he's winning! All other columns have been filled, and yellow has dropped one stone in column c, to which red responded with g1. Now yellow has to drop a stone and will lose. Again, we see that 4 in a row is an asymmetric game. Having two "wrong" threats is wrong for yellow, but right for red. It's easy to understand: If there is a threat on an odd row, it effectively changes the role of red and yellow, because an odd number of stones can still be dropped in that column. Therefore, if red has one threat in an odd row, he can win by creating another threat in an odd row. Of course, he can also win by creating a threat in an even row and giving up the threat in the odd row.
So the message is the following: Try to use your stones efficiently. Create threats in even or odd rows depending on whether you started or not. Multiple threats can be evaluated by first ignoring threats on even heights - they don't change anything for counting. For example, if yellow has a threat on an odd height, red should not play for one even threat. It won't change anything. Red will have to play for an odd threat, as this will reverse the roles of the two players. If red succeeds, yellow will have to give up his threat and the game will end in a draw.

Further Reading

James D Allen has written an article on expert play in 4 in a row. It explores the above ideas in (much!) more depth and with more Japanese words ;-) - it also gives you a list of the winning openings. Allen was one of the first two persons to solve 4 in a row. The other was Victor Allis. Velena is a DOS program which plays perfectly.
Written in march 2000 by Martin Fierz, 4inarow(a)fierz.ch. Comments on this tutorial are welcome!