Kraftmessung
Ich probiere in diesem Unterrichtsblock die Masse eines 10-Rappenstücks zu bestimmen - dabei lernen Sie wie man Kräfte messen kann, wofür Kraftmessungen eingesetzt werden können, was es für Sensortypen gibt und vieles mehr!Als Einleitung demonstrieren die nachfolgenden Videos 3 Varianten eines Experiments mit dem ich die Masse der Münze zu bestimmen versuche.
Ein erstes Experiment
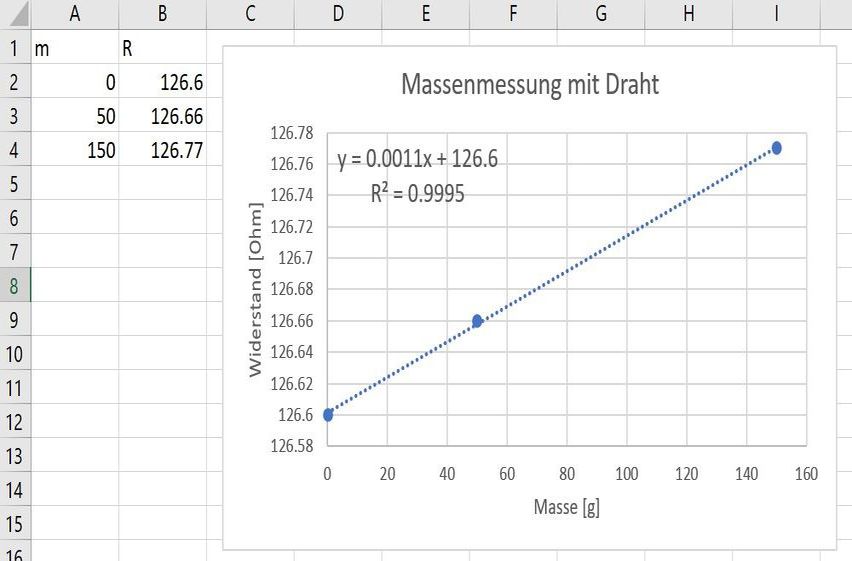
In einem ersten Versuch sehen Sie ein wichtiges Grundprinzip für Kraftmessungen - Kräfte führen zu Dehnungen die wiederum als Widerstandsänderungen detektiert werden können.Schauen Sie sich das Video an, und notieren Sie sich die Widerstandswerte für die 4 Zustände 0g / 50g / 150g / 150g + 10-Rappenstück.
Plotten Sie die Kennlinie dieses "Kraftsensors" in Excel, machen Sie einen geeigneten Fit und finden Sie damit heraus was die kleinstmögliche Masse ist die
man mit diesem Aufbau messen kann. Wie gut sind die Chancen dass wir damit die Masse des 10-Rappenstücks messen können?
Die Kennlinie ist zwar einigermassen linear, was immer schön ist, aber die kleinste messbare Widerstandsänderung von 0.01 \(\Omega\) entspricht einer Masse von 9 Gramm. Im Video hat man auch gesehen, dass beim Hinzufügen des 10-Rappenstücks keine signifikante Änderung
des Widerstands beobachtbar war - es ist wohl leichter als 9 Gramm, und der Drahtwiderstand ändert sich darum um weniger als 0.01 \(\Omega\) -
wir können also als erstes Resultat lediglich \(m < 9 g\) hinschreiben, und von 1% Messgenauigkeit sind wir noch weit entfernt.
Der Draht ist so dünn, dass er bei etwa 400 Gramm aufgelegter Masse bricht, d.h. wenn wir als kleinsten Messwert 9 Gramm messen können,
und als grössten Messwert 400 Gramm, dann hat unser System einen "dynamischen Messbereich" von etwa 1:40 - der grösstmögliche Messwert ist
40x grösser als der kleinste.
Lösung anzeigen
Der erste Versuch ist also wenig ermutigend - wie könnte man diese Messung verbessern?
Lösung anzeigen
Zweites Experiment
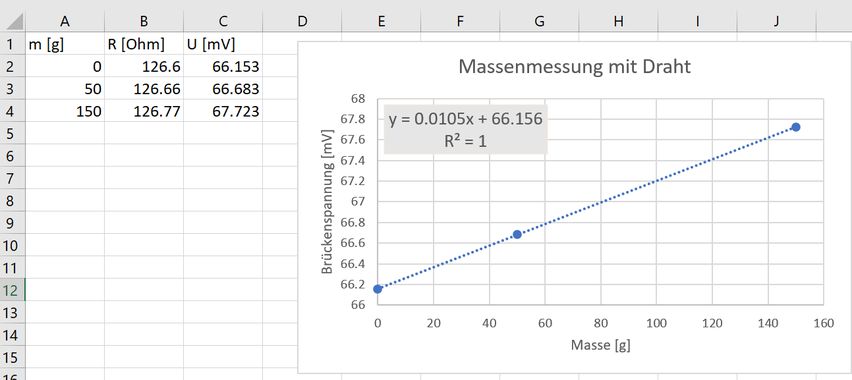
Der Versuchsaufbau aus dem ersten Experiment wird verbessert.Schauen Sie sich wieder das Video an, und notieren Sie sich wieder die Messwerte für die 4 Zustände 0g / 50g / 150g / 150g + 10-Rappenstück.
Plotten Sie die Kennlinie des verbesserten Kraftsensors in Excel, machen Sie wieder einen geeigneten Fit und finden Sie damit wieder
heraus was die kleinstmögliche Masse ist die
man mit diesem Aufbau messen kann. Wie gut sind diesmal die Chancen dass wir damit die Masse des 10-Rappenstücks messen können?
Die Kennlinie ist wieder ziemlich linear, und die kleinste messbare Spannungsänderung ist \(1 \mu V\). Aus der Gleichung für die Kennlinie
entnehmen wir dass 10.5 \(\mu V\) einem Gramm entsprechen, wir können diesmal also ziemlich genau Massenänderungen von 0.1 Gramm
detektieren (genau: 0.0953 Gramm entspricht 1 \(\mu V\)). Der dynamische Messbereich ist nun bereits von 0.1 - 400 Gramm angestiegen, also
statt 1:40 nun 1:4000 - der Einsatz der Messbrücke hat die Auflösung um einen Faktor 100 (!) verbessert.
Im Video hat man auch gesehen, dass beim Hinzufügen des 10-Rappenstücks die Brückenspannung von 67.723 auf etwa 67.743 mV steigt;
also um 20x0.0953 Gramm, und unser zweites Resultat ist m \(\approx\) 1.9g.
Ich habe \(\approx\) geschrieben, weil man im Video gut sieht dass die letzte Nachkommastelle auf dem Multimeter nicht stabil ist, und man
darum nicht genau sagen kann was für einen Wert man ablesen sollte.
Ganz abgesehen davon ist auch schon klar dass wir einen Digitalisierungsfehler von der halben Auflösung machen, d.h. mindestens
von 0.05g; von 1% Messgenauigkeit sind wir auch hier sicher noch weit entfernt.
Lösung anzeigen
Was könnten wir als nächstes tun um mit dem nicht ganz stabilen Messwert besser umzugehen?
Lösung anzeigen
Drittes Experiment
Der Versuchsaufbau aus dem zweiten Experiment bleibt gleich, aber wir verbessern unsere Methodik für die Messung!Schauen Sie sich wieder das Video an, und notieren Sie sich die Messwerte mit und ohne 10-Rappenstück. Beobachten Sie auch möglichst genau was das Messgerät anzeigt!
Die Kennlinie des Messaufbaus hat sich nicht verändert, aber wir haben ein neues, hoffentlich besseres Resultat. Berechnen Sie mit
den neuen Werten für die Brückenspannung wiederum die Masse des 10-Rappenstücks. Vergleichen Sie dann das Resultat mit der offiziellen
Angabe der Schweizerischen Nationalbank. Sind Sie zufrieden mit
dem Resultat? Können Sie erklären warum es nicht passt, bzw. was passiert ist dass Sie vermutlich unzufrieden sind?
Der Vergleich mit dem offiziellen Wert der SNB von 3.00g zeigt dass die "verbesserte" dritte Messung schlechter war als die zweite Messung,
obwohl sie doch hätte genauer sein sollen.
Lösung anzeigen
Haben Sie eine Vorstellung was bei der angeblich verbesserten Messung schief gelaufen sein könnte, und warum? Tipp: beobachten Sie das
Messgerät während den ersten 46 Sekunden des Videos genau!
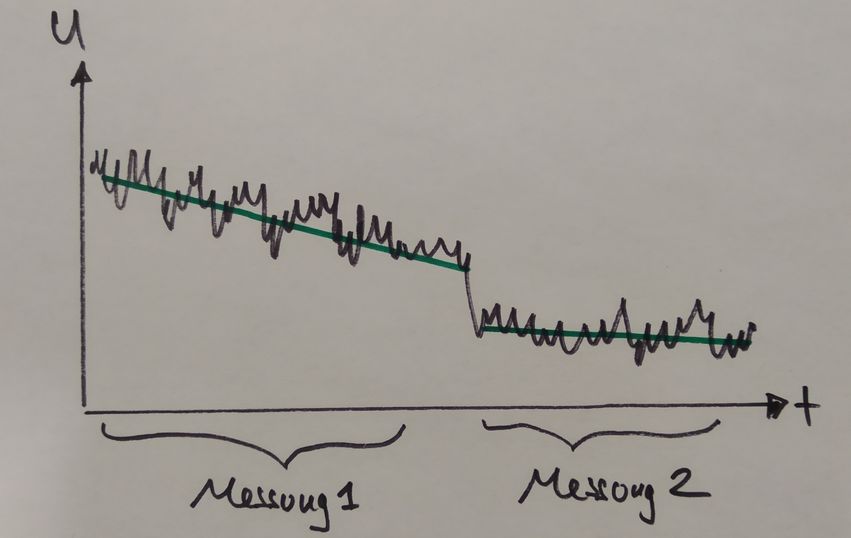
Wenn man die Messdaten - wie hier - nicht visualisieren kann, dann sieht man diesen Trend in der gemessenen Spannung nicht, und natürlich
ist die gemessene Spannungsdifferenz zwischen Messung 1 und Messung 2 zu gross, wenn ein derartiger Trend in den Daten ist. Die Mittelwertbildung
ist nur dann sinnvoll, wenn man wirklich Messdaten hat die aus einem stabilen Mittelwert + zufälligen Rauschen bestehen; bei einem zeitlichen
Trend hingegen nützt sie nichts, sondern schadet eventuell sogar. Merken Sie sich bitte dass die Mittelwertbildung zwar sehr oft nützlich
ist, aber nur wenn man sicherstellt dass es sich wirklich um Messdaten mit rein zufälligem Rauschen handelt!
Woher könnte nun dieser Trend in den Messdaten kommen? Hier kann man nur spekulieren, aber eine sehr naheliegende Spekulation hat mit
der Eigenerwärmung der Widerstände zu tun: Ich habe 5V Speisespannung angelegt, d.h. etwa 2.5V pro Widerstand, die Widerstände setzen also
eine elektrische Leistung von P = U2/R = 52mW um, und erwärmen sich dadurch. Da wir schon öfter gesehen haben dass Widerstände
temperaturabhängig sind, kann man sich leicht vorstellen dass sich die 3 fixen Widerstände in der Messbrücke erwärmen, und sich dadurch
das Spannungsniveau im Brückenzweig mit Widerstand+Draht leicht verschiebt, was zum beobachteten langsamen Drift führt. Der Draht selber
wird sich wegen seinem viel grösseren Oberfläche-Volumen-Verhältnis viel weniger stark erwärmen.
Lösung anzeigen
Wie gross müsste die relative Widerstandsänderung ΔR/R durch die Erwärmung etwa gewesen sein um etwa 0.022mV die "zu viel" waren zu erzeugen?
Tipp: Werte in Näherungsformel für die Viertelbrücke einsetzen!
Mögliche Verbesserungen der Methode wären z.B. die Speisepannung zu halbieren (halb so viel Signal, aber 4x weniger Eigenerwärmung), oder längere
Wartezeiten im Experiment um sicherzustellen dass sich die Widerstände im thermischen Gleichgewicht befinden.
Lösung anzeigen
Zwischenfazit
Wir haben bisher eine Messtechnik basierend auf der Widerstandsänderung eines gedehnten Leiters kennengelert, die mindestens ansatzweise funktioniert, von einer Messgenauigkeit von 1% sind wir aber noch weit entfernt. Wir haben ebenfalls bereits gesehen dass die temperaturabhängigkeit der elektrischen Widerstände Probleme bereiten kann, selbst winzige Widerstandsänderungen der Referenzwiderstände in der Messbrücke machen sich leicht bemerkbar als Drift im Messsignal, gerade weil die Messbrücke eben so empfindlich auf kleine Widerstandsänderungen reagiert.Natürlich ist diese Messtechnik mit einem langen brüchigen Draht völlig ungeeignet für einen produktiven Einsatz, aber das Prinzip wird genau so in sogenannten Dehnmessstreifen umgesetzt.
Theorie
Lesen Sie das nachfolgende PDF-Skript das die Theorie der Kraftmessungen mit Dehnmessstreifen erklärt - mit den oben behandelten Experimenten sollte es weitgehend selbsterklärend sein.
Ein Beispiel aus der Praxis
Dehnmessstreifen werden für ganz viele, sehr unterschiedliche Anwendungen eingesetzt. Ein Beispiel für den Einsatz von Dehnmessstreifen ist der Radlastcheckpoint der SBB: Bei diesen Anlagen wird ein Zug bei der Vorbeifahrt gewogen. Um diese Information im Betrieb zu messen, wurden an mehreren Stellen in der Schweiz die Schienen mit Dehnmessstreifen ausgerüstet, so dass man direkt sieht wie stark die Schiene sich verbiegt wenn ein Zug über sie fährt - die Schiene ist also zu einer Waage umfunktioniert worden! Im Bild unten sehen Sie wie das aussieht:

Die Masse des fahrenden Zugs wird dabei auf 1% genau gemessen - auch wenn er mit vollem Tempo darüber fährt! Das ist wichtig, da man natürlich nicht immer anhalten will, um den Zug auszumessen; das würde ja den Betrieb stören.
Mit Hilfe dieser Waagen kann man beispielsweise kontrollieren ob ein Güterzug das richtige Gewicht hat: ähnlich wie bei den Lastwagen wird im Güterverkehr der Preis nach Gewicht abgerechnet - wenn ein Zug aus dem Ausland die Schweiz durchquert, so muss umso mehr für die Fahrt bezahlt werden je schwerer er ist - dank den Waagen kann die SBB kontrollieren, ob die Angaben zum Gewicht stimmen.
Eine zweite wichtige Information die man aus der Messung bekommt, ist über die Qualität der Räder: bei Vollbremsungen schleifen die Räder über die Schienen und bekommen dadurch Flachstellen. Dadurch poltern die Rädern bei der Fahrt - mit jedem Mal wo die Flachstelle auf die Schiene kommt, gibt es einen Schlag auf die Schiene, die dadurch schneller altert. Aufgrund des zeitlichen Verlaufs des Signals vom Radlastcheckpoint kann man erkennen, ob so eine Flachstelle vorliegt, und dadurch den Wagenbesitzer auffordern, seinen Räder nachschleifen zu lassen.
Weiterführende Informationen:
Broschüre über Zugkontrolleinrichtungen der SBB (pdf)
- Skizzieren Sie wie ein Signal eines Radlastcheckpoints aussehen könnte wenn ein einzelner Wagen über den Checkpoint fährt.
- Wie würde sich das Signal eines Rads mit Flachstelle wohl von einem Signal eines runden Rads unterscheiden? Machen Sie auch dazu eine Skizze!
- Was könnte man für einen Algorithmus einsetzen um die Flachstelle zu detektieren?
Lösung anzeigen
Das Signal des Kraftsensors wird vermutlich etwa so aussehen wenn ein Wagen mit 2 Achsen darüber fährt:
Jede Achse verursacht beim Überfahren einen Peak auf dem Signal dessen Breite umgekehrt proportional zu der Zuggeschwindigkeit ist, und dessen Höhe proportional zu der Masse des Wagens ist. So kann man z.B. feststellen ob der Wagen asymmetrisch beladen ist, indem man die Signale auf beiden Schienen vergleicht.
Hat ein Rad eine Flachstelle, so wird es einen Schlag auf die Schiene geben = ein Kraftstoss. Das könnte dann so aussehen wie in dieser Skizze grün dargestellt:
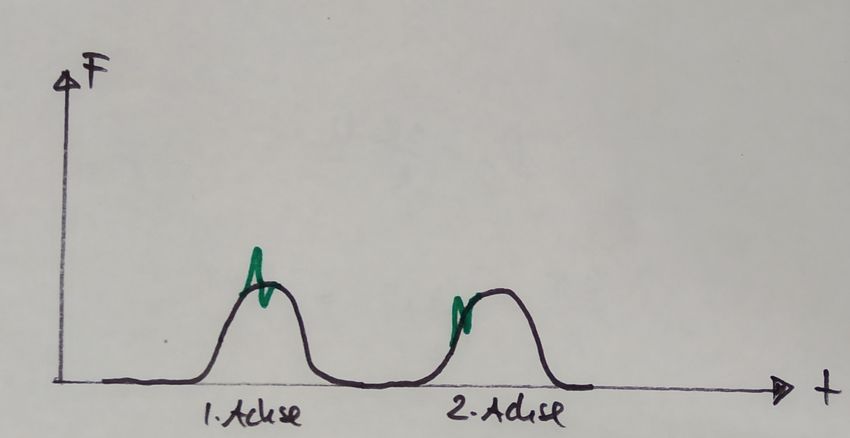
Da der Schlag als schnelles Signal auf einem langsamer veränderlichen Signal auftritt, sollte man ihn mit einem geeignet gewählten Hochpassfilter vom normalen Radsignal trennen können.
Der Radlastcheckpoint ist ein schönes Beispiel für eine Messung, bei der man nicht "ab Stange" eine Lösung einkaufen kann; sondern es war wichtig, dass die beteiligten Ingenieure die Grundlagen der Kraftmessung gekannt haben und ausgenutzt haben, und auch dass sie das Signal dann richtig verarbeitet haben!
Messung mit einer kommerziellen Wägezelle
Kommen wir aber zurück zu der Münze. Mit den einfachen Laboraufbauten und einem dünnen Draht konnte ich - nicht überraschenderweise - das Gewicht der Münze nicht so genau messen wie ich wollte. Ich nehme darum als nächstes richtige Dehnmessstreifen dafür: Im folgenden Experiment setze ich anstelle des Laboraufbaus eine kommerzielle Wägezelle (mit Dehnmessstreifen) vom Typ PW15AHC3 von HBM ein. Diese Wägezelle hat einen Messbereich von 0-20 kg. Dazu verwende ich einen teuren/edlen Messverstärker (ca. 10'000 CHF) - ob es damit wohl klappt?
Obwohl nun ein professionelles Messsystem eingesetzt wurde, hat die Messung wieder überhaupt nicht geklappt - nennen Sie zwei Gründe dafür!
Lösung anzeigen
Messung mit einer kommerziellen Wägezelle mit Trägerfrequenzverstärkung
Nach Experiment 4 ist man ein bisschen versucht aufzugeben - wer will schon wissen wie schwer eine Münze ist wenn man das doch einfach nachlesen kann? Und warum setzt der Dozent auch eine Wägezelle für bis zu 20kg ein für diese Aufgabe, das ist doch offensichtlich dumm!In Experiment 5 demonstriere ich dass es tatsächlich möglich ist die Masse der Münze mit dieser Wägezelle auf 1% genau zu messen, indem die Messbrücke mit Wechselspannung statt mit Gleichspannung betrieben wird. Dieser scheinbar winzige Unterschied im Betrieb erhöht die Messgenauigkeit um mindestens einen Faktor 10, da die Elektronik nun nur noch spezifisch die Amplitude des Signals bei der (ihr bekannten) angelegten Frequenz auswertet, und dadurch Störsignale bei allen anderen Frequenzen unterdrückt. Wir haben diese Technik letzte Woche bei der Frequenzanalyse bereits kennengelernt. Wenn Sie noch mehr darüber wissen wollen, lesen Sie den Wikipedia-Eintrag dazu.
- Schauen Sie im Video nochmals genau auf den Berechnungskanal und bestimmen Sie die Masse der Münze aus der Messung der einzelnen Münze. Was bekommen Sie für eine Masse? Wie stark schwankt der gemittelte Messwert etwa (= was wäre die kleinste Massenänderung die wir so messen könnten?)
- Schauen Sie im Video nochmals genau auf den Berechnungskanal bei der Messung von 10 Münzen - was bekommt man dort für eine Masse?
- Die Trägerfrequenzverstärkung hat auch einen Nachteil gegenüber der DC-Messung. Können Sie sich vorstellen was der Nachteil sein könnte? Tipp: im Video bei 1:14 ganz genau hinschauen!
Lösung anzeigen
- Bei der Einzelmessung lese ich aus dem Video beim Berechnungskanal beim ersten Mal (ca. 2:40 im Video) 0.22g -> 3.28g ab, beim zweiten Versuch (ca. 3:00) im Video) 0.20g->3.23g, d.h. die erste Messung ergibt 3.06g, die zweite 3.03, oder gemittelt 3.045g, schon ein sehr guter Wert.
- Die blaue Kurve schwankt in der Grafik meistens nur um +-0.02g (z.B. bei 2:33 im Video), wir können also mit einer Wägezelle, die bis zu 20 kg messen kann, auch noch Änderungen von 0.02g sehen - ein dynamischer Messbereich von 1:106!
- Bei der Messung der 10 Münzen lese ich 30.41g ab (ca. 3:43), ohne Münzen 0.18g (3:58), das ergibt 30.23g für alle Münzen oder 3.023g für eine Münze, das ist weniger als 1% Abweichung zum offiziellen Wert der SNB.
- Die Trägerfrequenzverstärkung ist unglaublich cool, aber sie hat einen kleinen Nachteil: um die Amplitude der AC-Spannung auszuwerten muss man mindestens über eine Periode des Signals integrieren, und darum ist die Zeitauflösung mit dieser Methode beschränkt. Will man ganz schnelle Messungen machen, muss man die Trägerfrequenz erhöhen, oder eben wie im Fenster das im Video zu sehen ist - doch mit DC messen.
Warum funktioniert die Trägerfrequenzverstärkung?
Im folgenden Video zeige ich Ihnen anhand von einem verrauschten Sinussignal am Oszilloskop warum die Trägerfrequenzverstärkung so gut funktioniert. Ich werde dabei die Amplitude von einem verrauschten Sinusssignal messen. Man kann dies auf verschiedene Arten tun; beispielsweise kann man die Spitze-Spitze-Amplitude messen, oder den Effektivwert des Signals, oder eben die Amplitude der Fouriertransformation bei der Frequenz des Sinus. Notieren Sie sich beim Schauen des Videos die 3 Messwerte (Spitze-Spitze, Effektivwert, Maximum Fouriertransformation) bei 0%, 20%, 40%, 60%, 80% und 100% Rauschen.
Sie haben sich den Spitze-Spitze-Wert, den AC-RMS-Wert sowie das Maximum aus der Frequenzanalyse für die 6 Werte 0,20,40,60,80,100% Rauschen abgeschrieben aus dem Video. Machen Sie in Excel einen Plot der 3 Werte als Funktion des Rauschens; machen Sie auch den Spitze-Spitze-Wert vergleichbar mit den beiden anderen Werten indem Sie ihn durch \(\sqrt 8 \) dividieren (und stellen Sie sicher dass Sie verstehen warum ich durch \(\sqrt 8 \) dividiert haben will!).
Lösung anzeigen

Was schliessen Sie aus der Grafik?
Lösung anzeigen
Zusammenfassung
Zum Schluss ist es mir tatsächlich gelungen die selbstgestellte relativ absurde Aufgabe zu lösen - aber obwohl die Aufgabe etwas absurd war, haben Sie hoffentlich auf dem Weg doch einiges gelernt:- Das Messprinzip von Dehnmessstreifen, die die Default-Lösung für präzise Kraftmessungen sind, und auch in vielen Waagen verbaut werden.
- Der Einsatz von Messbrücken zur empfindlicheren Messung von Widerstandsänderungen wurde repetiert
- Die Mittelwertbildung als Methode für genauere Messungen wurde repetiert, und es wurde auch gezeigt wann/warum das manchmal nicht funktioniert.
- Der Einsatz von einem Datenerfassungssystem wurde gezeigt mit dem man Daten erfassen, visualisieren, mitteln, und speichern kann, und Sie haben hoffentlich gesehen wie viel mehr man dabei sieht als wenn man nur auf das Multimeter schauen kann!
- Die Trägerfrequenzverstärkung wurde demonstriert, und dabei wurde zum Schluss eine eigentlich fast unglaubliche Präzision erzielt - der dynamische Messbereich von Experiment 1 von etwa 1:40 wurde im Experiment 6 auf 1:106 erweitert! Weil Kraftsensoren so unglaublich genau arbeiten können, kann man auch andere Messungen auf Kraftmessungen zurückführen, beispielsweise Füllstandsmessungen.
PS
Piezosensoren
Ich habe mich hier auf Dehnmessstreifen konzentriert - es gibt noch eine weitere wichtige Technik der Kraftmessung, die Piezosensoren. Ganz grob gesagt kann man mit den DMS keine schnellen Kraftänderungen messen, da das Element auf dem die DMS angebracht sind, ein bisschen federn muss, und somit schwingungsfähig ist; Frequenzen oberhalb der Eigenschwingungsfrequenz dieses Systems werden mechanisch gedämpft und können damit nicht mehr gut erfasst werden. Piezosensoren messen Kräfte direkt im Sensor (nicht über einen Federkörper), und bestehen aus sehr starren Kristallen die viel höhere mechanische Eigenfrequenzen haben - damit kann man darum schnelle Vorgänge messen. Typische Grenzfrequenzen von Systemen mit DMS sind im Bereich von ca. 100-1000 Hz. Piezosensoren sind aber weniger genau, und wenn man die Geschwindigkeit nicht braucht, so sind DMS besser geeignet.In der Schweiz gibt es die Firma Kistler, die solche Sensoren herstellt, und damit unter anderem - ganz ähnlich wie bei den Radlastcheckpoints der SBB - Fahrzeuge auf Strassen beim Vorbeifahren misst (Weigh In Motion). Wenn es Sie interessiert können Sie bei Kistler mehr darüber lesen.
Anwendungen
Kraftsensoren haben sehr viele Anwendungen, und hier sollen noch ein paar Beispiele genannt werden: Neben Kräften kann man auch Druck, Beschleunigung und Drehmomente messen. Die typische Anwendungen der Kraftmessung ist sicher das Wägen von Objekten, wie für fahrende Züge und Fahrzeuge gezeigt. Man kann auch den Füllstand eine Silos mit Schüttgut drin messen, indem man das Silo auf Kraftsensoren stellt (falls Sie sich gefragt haben wofür der 1000-Tonnen-Sensor gut ist...). Kraftsensoren werden auch in den Auffangnetzen oberhalb von Strassen/Schienen verbaut, damit man detektieren kann wann ein Steinschlag stattfindet, und nach dem Ereignis das Auffangnetz kontrollieren gehen kann. Ich habe mit einem Kraftsensor auch schon Verdunstungsraten von Wasser gemessen (Abnahme der Masse über die Zeit), und in einem lustigen P6-Projekt EIT hat eine Viererbob-Mannschaft ihren Bob mit Kraftsensoren in den Griffen ausrüsten lassen, damit sie sehen konnten wer wann wie viel schiebt.
Die Gewichte unserer Münzen
Ich war übrigens nicht sicher dass die Angabe der SNB zu den Münzengewichten stimmt. Bei allen Münzen ist die zweite Nachkommastelle 0: 5 Rappen sind 1.80g schwer, 10 Rappen 3.00g, 20 Rappen 4.00g, 50 Rappen 2.20g, 1 CHF 4.40g, 2 CHF 8.80g und 5 CHF 13.20g.Ich habe mir überlegt: Entweder ist das ein Riesenzufall, oder die Münzen werden extra so gemacht, oder die Münzen wurden mit einer Waage gewogen die nur eine Nachkommastelle anzeigt, und jemand hat eine Stelle zuviel angegeben was man eigentlich nicht sollte. Mir erschien die Variante mit "eine Stelle zuviel angegeben" am Wahrscheinlichsten. Aber "erscheint" ist ja nicht gut genug wenn man es genau wissen will...
Eine Nachfrage bei der SNB hat ergeben: Unsere Münzen waren ab 50 Rappen aufwärts ursprünglich Silbermünzen, d.h. der Wert der Münzen war durch ihr Gewicht gegeben als Wert des Silbers in der Münze. Darum ist der Zweifränkler genau doppelt so schwer wie der Einfränkler, und der wiederum doppelt so schwer wie die 50-Rappen-Münze. Die Gewichte der Münzen waren also tatsächlich überhaupt nicht zufällig, sondern mussten genau aufeinander abgestimmt sein damit die Werte der Münzen zueinander gepasst haben. Der Fünfliber passt nicht in dieses Schema, aber er war bis 1928 noch grösser und schwerer!
Ich habe dabei auch gelernt dass die Nationalbank keine Toleranzen zu den Münzen angibt, vermutlich um Falschmünzern nicht zu sagen wie genau sie das Gewicht nachmachen müssten. Und als Letztes habe ich dabei noch gelernt dass die zufällig gewählte 10-Rappen-Münze die ich hier ausgemessen habe, die älteste im Zahlungsverkehr stehende Münze der Welt ist. Sie besteht in dieser Form schon seit 1879!

