Evaluation functions
I started programming checkers at the end of 1996 when I had finished my Physics studies and didn't quite know what I should do next, and while I was trying to figure that out, I spent some time writing a checkers program (I was motivated by having read about the Tinsley-Chinook matches). Sometime later, about 1999, I split the interface and the checkers engine - or the brain of the program - in two parts, creating CheckerBoard and Cake. In the beginning, I was reading Jim Loy's checkers pages (sadly gone now?) to learn about checkers and to write an evaluation function. Every game playing program needs an evaluation function, which tells it how good a given position is. Traditionally, this is hand-crafted by human experts. In checkers, you could imagine giving a certain number of points (say 100) for each man, more points (say 130) for each king, and then far less points for some positional factors - for example, how strong your back rank is. Figuring out such patterns (or features to evaluate), and giving them the correct number of points (or weights) used to be more of an art than a science, and programmers often went by gut instinct. To give you one example, in checkers the formation of black men on 5,9,13 against white men on 14,17,18,22 is something white wants to avoid: 
White cannot move these 4 men any more - 18-15 immediately loses to 9x25, whereas 14-10 allows 9-14 18x9 5x21, winning a man for red. Recognizing this pattern in a checkers program is actually very easy - you just write a line of code that checks if there are three red men on 5,9,13, and another to find out if there are 4 white men on 14,17,18 and 22. Then, you use your gut feeling to give red some points for having achieved this formation. How much should this be worth? In this example, it actually is about as good as being a whole man up, so you could be tempted to give 100 points to red. However, sometimes there are additional tactics around, so maybe somehow white can escape from this formation - and then it's worth nothing having it. So let's say we choose a middle ground and come up with 50 points for this formation. Now you need to decide whether or not adding this knowledge is any good.
Test positions
In the old days of game programming, this was done with test positions. Let's say that you had observed your engine losing a game because of this formation, then you go to a position before this formation occurs and see if the engine will now play better. This method of using test positions was very popular in the 1970's and 1980's and of course I also used it whenever I came across interesting positions. However, when you start to tune a parameter to just work in one or a few positions, things can go really wrong. Imagine that you need to tune the penalty up to 100 points to avoid your engine from making a losing move in your wonderful test position. It may now work in this particular position, but will it actually help in your average position? What if white has a man on 21 so the described 2-for-one shot doesn't work? Will you be making your engine go mad and lose some games in return for not losing in the one single test position you had looked at?Engine matches
To find out, you have to play a lot of games and see if your engine performs better than before. I implemented an "engine match" feature in CheckerBoard, where two engines play a 288-game match against each other, and CheckerBoard keeps track of the result (288 games because the 144 openings of the ACF 3-move deck are played with both colors). Ed Gilbert and I used this extensively to improve KingsRow and Cake in the following years - we would tinker with our engines, adding knowledge (more features in the evaluation), testing the effect in a match, adjusting the weights, and so on. I used to watch the games and try to figure out if and why Cake lost, and tried to understand what kind of knowledge was missing. I remember when Ed once figured out that "tailhooks" are something good - a king hanging on to the "tail" of two men and thus immobilizing them (e.g. white king on 11, black men on 15 and 18). I had not figured this out yet, and because Ed gave a bonus for this feature, KingsRow suddenly started winning some games with this pattern repeating over and over again. Of course, seeing it often enough I figured it out too, I added the knowledge, and those embarassing losses disappeared again. There is also a lesson to be learned here: even if some patterns hardly ever show up in the games because both sides know that they need to avoid them, the knowledge is still important and must be there. Just looking at high quality games, you might be missing some patterns that experts are good enough to avoid, but which you should still know!
Perfect and near perfect knowledge, and near perfect programs
The knowledge encoded in the evaluation function is obviously far from perfect. It just has to work more than half of the time to be a net gain in playing strength. In checkers, we used and still use two other pieces of knowledge which are much better: Endgame databases and opening books. The endgame databases can be computed "mathematically" and will give perfect knowledge on whether a given position is a win, loss or a draw. I computed the 8-piece endgame databases during my postdoc in Hawaii in 2002, shortly before the world computer checkers championship in Las Vegas; and of course the Chinook team had done so long before. With those 8-piece endgame databases available, and my otherwise also quite formidable engine, perfected over hundreds of engine matches, I set out to compute an opening book using techniques I had learned from Thomas Lincke. An opening book will tell the engine which move to play in the starting phase of the game, without actually thinking. In "One jump ahead", Jonathan Schaeffer describes how he had tediously entered opening lines from checkers books into his opening book for Chinook, and how sometimes there had been mistakes in the human books, and how transpositions were tricky etc. It must have been terrible - and fortunately, using strong checkers engines, the whole process of figuring out which moves are best in the opening can be automated. For the 2002 computer checkers world championship in Las Vegas I was a bit late - I had only had the 8-piece databases available for a few weeks, and had only managed to compute about 100'000 opening positions, and Cake got into trouble in some games in the opening, and lost two of 48 games in Las Vegas - ending up in third and last place. I used some of the mistakes made in Las Vegas as test positions, figured out some further improvements in the search algorithms (resulting in Cake Sans Souci, probably the world's best checkers engine in 2003), and went on to compute an enormous opening book (with 2 million moves instead of 100'000) using 3 high-end PCs of the time computing 24/7 for about a year or maybe two. For the planned next computer checkers world championship in Manchester, I would have been more ready than Las Vegas, but it was cancelled for reasons I have forgotten. Ed and I both wanted to see where we stood, and in late 2004 each of us played an engine match with 312 games, with Cake 1.7 ("Manchester") winning 3-1 with 620 (!) draws against Ed's KingsRow version of that time. That was more or less the moment where my interest in computer checkers started waning - the engines appeared to be playing nearly perfectly (losing a single game in a 624-game-match is quite a feat!), and all that was left to do was to create ever larger endgame databases and opening books - the fun of discovering new features to add to the evaluation, or better search algorithms was more or less gone. With no further computer checkers world championships coming up, I hardly worked on my engine any more for a while. I found a bit of motivation in 2007/2008 to create Cake 1.8, and in 2011 to create Cake 1.85, but I think both were rather small changes compared to Cake Manchester. Development of Cake went into hibernation, and I thought I would probably never work on it again. I thought it was probably close to perfection and there was no point in working further on it.Ed Gilbert uses Machine Learning!
Then, towards the end of 2018, about 8 years after development of Cake had ended, I happened to come - quite by chance! - across the news that Ed Gilbert had made a new much improved version of KingsRow and released it in November 2018. You can read more about it in the Checker Maven. In short, Ed had done away with his traditional evaluation function with human-devised patterns and trial-and-error-tested weights as described above, and had used a very different approach for creating a far better evaluation function (which he learned about from Fabien Letouzey, famous for changing chess programming forever with his open source program "Fruit"; Fabien had used this pattern-based evaluation approach in his international draughts program Scan. I think he got the idea from the Othello programming community, but I am not sure). His approach worked as follows: First, he split the board into several smaller areas - imagine for instance that you just make 4 quarters of the board with 4x4 squares, i.e. 8 squares where pieces can actually move to (in fact, he used a different partitioning of the board, but that's not important for the moment). For each of those 8 squares, you can have either an empty square, a man of either side, or a king of either side, which means there are 5 to the power of 8 legal combinations of pieces that can be on those squares - or 390'625 combinations. In fact, not all of these are legal, as on the red back rank you cannot have white men so there are less - "only" 250'000 possible legal positions. As a next step, he created an evaluation function which gave each of those 250'000 patterns a unique number of points or weight. Instead of having just a few dozen features like we had earlier, inspired by human knowledge of checkers, he now had hundreds of thousands of features, each with its own weight. It seems as if you would need 4 x 250'000 weights, as you have 4 quarters of the board, but in fact the evaluation has a symmetry - the white single corner and the red single corner should have the same weights with colors reversed, so there are "only" 2x 250'000 weights. It's obvious that with such a huge number of weights, you can encode much more information than a traditional evaluation function ever could. The beauty of this approach is that the evaluation is also super-fast to compute, as you just need to calculate an index and do a table lookup. Of course there is a downside though - you need to find the correct weights for those hundreds of thousands of features, and obviously you can't tinker around with so many weights, running multiple engine matches to find the correct weight for each parameter - each engine match might take an hour, and running millions of engine matches takes longer than a human lifetime, so a different approach is needed. That's where machine learning comes in handy.Logistic regression
The idea of automatically tuning evaluation functions is not new at all (and in fact that's not really surprising, since it is something which takes a lot of time to do manually). As far as I know, Michael Buro was the first to apply a technique called logistic regression in the 1990s for his Othello program Logistello, but also as far as I know, it didn't really catch on all that much. As far as I know, it only became popular after Peter Österlund wrote a post on the computer chess club on "Texel's tuning method", later also explained on the chess programming wiki. The general idea is that you can test an evaluation function based on a lot of labelled positions. If you have for instance 100'000 games, you can attach the labels win, loss and draw to each of the positions based on the outcome of the corresponding game. A checkers game might have around 30 positions, so you end up with 3 million positions with labels that way. Next, you take your evaluation function and try to change the weights of your features in such a way that the evaluation function gives the best agreement with the actual game results. The specific recommendation of Buro was to use a "logistic regression", where you take the score of the evaluation function and map that onto the range of values from -1 (loss) to 1 (win). You do this by using the "logistic function"f(score) = 2/(1+e-c*score) - 1.
If the score is goes to infinity,
the exponential goes to 0, and you get f(infinity) = 1; if the score goes to -infinity, the exponential is
infinite, and you get f(-infinity) = -1. Just looking at the function definition it's not obvious, but it's an
odd function (i.e. f(x) = -f(-x)), and you can see what it looks like in the graph below.
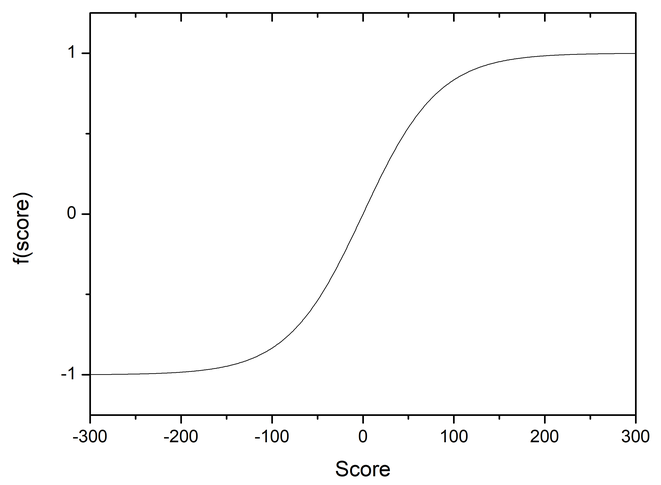Essentially, the logistic function is taking a point score of the engine, and translating it into a winning probability.
For example, with the constant c=0.024 as chosen by me, a score of 100 points (one checker up) is supposed to give you a
winning probability of 83%, a score of 200 points is a 98.4% winning probability.
Now, for all your labelled positions you calculate the score, calculate the winning probability based on the
score and take the difference to the actual game result; and using a typical least squares approach you sum up the
squares of those differences. If you have a position with score 100 which unsurprisingly lead to a red win,
you would calculate a 0.83 winning probability, a 0.17 difference to the result (win = 1), and that would give
a value of 0.17 squared = 0.0289 to be added to the grand total. Mathematically speaking, you would write
error = Σ (f(scorei) - resulti)²
While this looks kind of complicated, and while you still need to calculate a few million evaluation scores to figure out the error, this only takes about a second on a modern PC. You can now fiddle with the different weights in your evaluation function, and see if they improve (reduce) the error. If yes, keep the change, if no, revert to the old weight. It is still quite a daunting task to optimize hundreds of thousands of weights simultaneously (you can't just tune one weight at the time, but need to use a technique such as gradient descent), but it is far easier to handle than running hundreds of thousands of engine matches.
Ed did exactly this with KingsRow, tossing his handcrafted evaluation out of the window, and the result was KingsRow 1.18f.
Bob Newell wrote something on this engine in the
Checker Maven, but when it came to playing strength,
he used the techniques of the 1970's and '80s, showing what this engine was capable of in just three test positions - and in
fact, as far as I can see, test positions that any decent engine would get right anyway.
As you know by now, test positions are not the right way to judge an engine's strength - instead, i
ran 11-man-ballot engine matches with 4800 games at bullet speed (0.1s/move) against Cake 1.85
and got the following results:
Cake 1.85 - KingsRow 1.18 : 861 wins, 639 losses, 2232 drawsThe difference is absolutely enormous, and it may even be bigger because I was using an 11-man-ballot list with a few lost openings. When I saw this, I realized exactly how big the difference was, and decided to try something similar myself.
Cake 1.85 - KingsRow 1.18f: 241 wins, 1149 losses, 3410 draws (40.5% win rate)
Optimizing a handcrafted evaluation function
Of course, I could have done the same thing as Ed did straight away. It probably would have worked, but then just repeating what he did seemed like a futile excercise. Ed is a better programmer than I am, and he currently has more time for checkers programming too, so I couldn't really hope to compete with him any more. I therefore decided to do something different to start with - to just optimize the handcrafted evaluation function of Cake, by optimizing the many weights that I had adjusted by hand. This seemed like a fun project which could also be handled with the little time I can find for checkers these days - and also something interesting, because I could compare how well I had hand-tuned my evaluation function, and if and where I had made mistakes. Whatever weight values would show up in my optimized evaluation could also be interpreted by humans, as they are attached to human concepts of the game. In contrast, Ed's hundreds of thousands of weights are more or less meaningless to humans - we just don't think like that, we think in patterns, and recognize patterns.I started out by first generating games - as mentioned, a bullet engine match generates 4800 games, with about 30x more positions, so around 150'000 positions. Hungry for results, at first I didn't expose all of the parameters of my evaluation function to my optimizer which varies the parameters, searching for a lower error, but only about 25 which I thought were most important. With 150'000 positions to optimize 25 parameters, I would have thought that this would work wonders - but in fact, the result was frustrating, the engine with the "improved" evaluation was playing worse than the handtuned version. I nearly gave up then and there, but luckily, generating more games is easy (play another match with the new version, optimize with the 10'000 games you have now, play another match, optimize more, and repeat). After I had 20'000 games, the optimized version was about as good as my handtuned version, and from there on, it continued to improve. In the end, I had about 8.3 million positions, and 379 evaluation weights to tune, and the result of this was Cake 1.86.
So how good is Cake 1.86 compared
to Cake 1.85? Was it really worth it? Here are the same bullet match results against the two
KingsRow versions:
Cake 1.86 - KingsRow 1.18 : 970 wins, 567 losses, 2195 drawsI also ran a match of Cake 1.86 against Cake 1.85 - in the standard 3-move ballot match with 288 games, like I used to test earlier, at 1s/move
Cake 1.86 - KingsRow 1.18f: 258 wins, 866 losses, 3676 draws (43.7% win rate)
Cake 1.86 - Cake 1.85: 42 wins, 16 losses, 230 draws.
So overall, even though Cake 1.86 was still far worse than Kingsrow 1.18f, it is really a lot better than Cake 1.85 was. I don't think I ever made such a large improvement in Cake's playing strength within just 2 months, it was an interesting and fun project!
Cake 1.87, 1.88, 1.88d, 1.88q, 1.89d
After having spent a lot of time on the evaluation I decided to have a closer look at the search of Cake. Many of the mechanisms of the search depend on the evaluation too, and if you change a lot in the evaluation, it may well be that some things that used to work don't work any more or vice versa. I tinkered a lot with the search over the Christmas holidays 2019, and the result was Cake 1.87.After this, I tinkered with the search, hashtable replacement schemes and the evaluation some more and the result of that was Cake 1.88 (Summer 2020).
Cake 1.88 had about 400 parameters in its evaluation function, 256 of which were the "back rank" evaluation, where a value is assigned to each possible combination of black men on squares 1-8 (and correspondingly, the same value to the white men on squares 25-32). Since those are 8 yes/no informations, you get 28 = 256 possible parameters. For Cake 1.88d, I switched to a back rank evaluation that looked at the last 3 instead of the last 2 ranks, so squares 1-12 for black; which increased the number of parameters to 4284. This gave another small but clear improvement over 1.88.
For Cake 1.88q, I used a larger pattern (a 531441-Array for a dual-color 3-backrank evaluation) for the first time, so the number of parameters that it can use is now theoretically over half a million, but "only" about 10% of these are actually used - this is now very similar to what Ed did for KingsRow, except that Cake only uses one pattern instead of multiple patterns.
Finally, for Cake 1.89d I added 3 further patterns for positions with kings, each with 250'000 possible parameters. Overall "only" about 200'000 parameters are used though. This version is now very similar to KingsRow, except that it retains parts of the earlier handcrafted evaluation function.
To test the engine changes, I switched to the 11-man drawn deck, as determined by Ed Gilbert. This has a bit less starting positions than the deck I had used to create Cake 1.86; all lost 11-man-openings were removed by Ed. To be able to compare the result a bit better, I replayed the bullet match of Cake 1.86 - KingsRow 1.18f on this deck, and then compared it with the result of Cake 1.87 and 1.88 (0.1s/move on a Core i7-8650U; 128MB hashtable, 1280MB db cache):
Cake 1.85 - not tested with this deck, only full 11-man-deck (40.5% win rate) Cake 1.86 - KingsRow 1.18f: 178 wins, 757 losses, 3571 draws (43.6% win rate) (June 2019) Cake 1.87 - KingsRow 1.18f: 231 wins, 540 losses, 3735 draws (46.6%) (January 2020) Cake 1.88 - KingsRow 1.18f: 286 wins, 493 losses, 3737 draws (47.8%) (July 2020) Cake 1.88d- KingsRow 1.18f: 311 wins, 454 losses, 3741 draws (48.4%) (August 2020) Cake 1.88q- KingsRow 1.18f: 368 wins, 417 losses, 3721 draws (49.5%) (January 2021) Cake 1.89d- KingsRow 1.18f: 529 wins, 190 losses, 3787 draws (53.8%) (March 2021)As you can see from the results above, some of the changes were more relevant than others; with the first optimization of my handcrafted eval (Cake 1.86), improvements to the search (Cake 1.87) and the introduction of many more patterns (from 1.88d -> 1.89d) being the changes with the largest benefits.
Of course, Ed did not stop at KingsRow 1.18f, and improved KingsRow further; its current version is 1.19c and the latest "heavyweight" match of Cake 1.89 vs KingsRow 1.19c ended with
Cake 1.89d- KingsRow 1.19c: 366 wins, 243 losses, 3897 draws (51.4%) (March 2021)I also tested it against Jon Kreuzer's interesting GuiNN in version 2.05 (with endgame database support added by Ed Gilbert):
Cake 1.89d - GuiNN 2.05: 659 wins, 202 losses, 3646 draws (55.1%) (March 2021)Finally I looked at how this new engine does against my old hand-tuned engines. I tested against 3 different engines; Cake Sans Souci which I think was the world's best checkers engine back in 2003; Cake 1.81 is from the year 2009, a time where I had given up checkers as being boring or close to solved, and finally Cake 1.85 is from the year 2011, and was the last version of Cake before I started developing the machine-learned versions. I decided to match those engines against the very latest Cake 1.89d in a 288-game match (3-move deck, played with both sides), at 1s/move on my laptop; which is similar to the 5s/move matches I used to play 10-15 years ago. These matches show very drastically just how incredibly much better the machine-learned Cake is than the last handtuned versions:
Cake 1.89d - Cake Sans Souci 1.04k: 73 wins, 0 losses, 215 draws Cake 1.89d - Cake 1.81: 55 wins, 0 losses, 233 draws Cake 1.89d - Cake 1.85: 42 wins, 1 loss, 245 drawsThe results are extremely lopsided, and it's hard to understand how much stronger the machine-learned engines are. To find out, I ran engine matches with time handicap: Cake 1.89f was running at 0.1s/move, and Cake Sans Souci was running at 3x, 10x, 30x, 100x, 300x that amount of time. At about 100:1 time handicap, the engines are approximately equal. To better understand what an enormous improvement those machine-learned engines represent, it might be worth noting that Cake 1.8x (and the last handtuned version of KingsRow) were far better than the last computer world champion, Nemesis, which in turn was far better than the famous Chinook was, i.e. those were really really good checkers engines - but just very weak compared to what is possible with machine learning.
The white doctor
I wrote above that test positions are an outdated way of assessing a program's playing strength. Nevertheless, they can be interesting, especially if you don't try to tune your program to solve them. In this case, the tuning of the evaluation function was automated, and knew nothing about any test positions I could think of; so it is interesting to ask if any effect of the evaluation tuning can be seen in test positions. The most stunning example is the White Doctor opening. After the moves 1.12-16 22-18 2.10-14 24-20 this feared opening arises.
Surprisingly to a checkers novice like me, the only move that will not lose is 16-19, giving up a man after just two moves.
In his book on the Chinook project - "One jump ahead"- Jonathan Schaeffer writes about this position that "...the obvious moves are reputed to lose although this has never been proven. The seemingly worst move on the board (16-19), blindly throwing away a checker, does indeed draw. The analysis is difficult and quite deep. It took human analysts several decades to convince themselves that there is ineed a draw to be had. Given this position Chinook has no hope of finding the right move even with a week's worth of computing, let alone the average of two or three minutes that you are allowed in a tournament game."
Of course, Chinook was running on much slower hardware than today's computers, so you can probably replace the 2-3 minutes of back then with 2-3 seconds of computing on a modern PC; and the "week's worth of computing" with about an hour of computing on a modern PC.
I always found it an interesting position and often tried it with new versions of Cake - and it did a lot better than Chinook, needing typically about one minute (give or take a factor 2 depending on the version) to find 16-19. But of course, on old Chinook-style hardware it would also have had no hope of finding the correct move in the 2-3 minutes under tournament conditions.
Now compare what adding machine-learned evaluation functions can achieve in the white doctor position (with Cake 1.86, 1.87 - 1.89f are similar):
depth 1/5/2.3 time 0.00s value=-20 nodes 44 4kN/s db 0% cut 88.9% pv 16-19 23x16 depth 3/11/6.8 time 0.00s value=2 nodes 495 49kN/s db 0% cut 96.6% pv 16-19 23x16 14x23 26x19 8-12 depth 5/15/8.7 time 0.00s value=0 nodes 1887 188kN/s db 0% cut 97.1% pv 16-19 23x16 14x23 27x18 8-12 32-27 12x19 27-23 depth 7/19/10.8 time 0.00s value=4 nodes 5723 520kN/s db 0% cut 96.0% pv 16-19 23x16 14x23 26x19 8-12 25-22 11-15 19x10 depth 9/26/13.3 time 0.01s value=-2 nodes 29841 1865kN/s db 0% cut 95.0% pv 16-19 23x16 14x23 26x19 8-12 25-22 4- 8 22-18Cake finds the right move at depth 1, within 0.00s, i.e. even on Chinook-type hardware it would have been easily possible to find 16-19 within a fraction of a second if a program had had such a machine-learned evaluation function (Of course, KingsRow 1.18f also finds this on depth 1!). Of course, creating such machine-learned evaluations also needs a lot of computing power, which was not available 30 years ago.
Note that Cake sees no way of gaining back that man that it sacrifices, and also its two last main lines contain moves that would in fact lose (after 16-19 23x16 14x23 26x19 8-12 25-22 red must go 6-10 (which Cake 1.86 will again see within 0.00s when you give it that position) - but this is beside the point. It's impossible to see that red is winning the man back within fractions of a second; what makes Cake able to solve this position so fast is that the evaluation sees that there is lots of compensation for red.
I remember how I tried to add evaluation features that would somehow detect compensation for being a man down, and how it never really worked out - I never could make Cake solve the white doctor position really fast - and now, the automated tuning has been able to find what I couldn't all by itself.
So all this is very nice, but what I said above about test positions above also applies here: one great result in one test position is meaningless. There are many other hard openings where neither Cake or even KingsRow can find the right moves even when given many minutes of thinking time.
What about my handtuned evaluation weights?
Finally, I mentioned earlier that optimizing my handtuned weights would allow me to compare the automatically determined weights with those that I had figured out by myself and see where I went wrong, or where I was right. This comparison is actually not at all straightforward for two reasons:- I made minor changes to the evaluation function during the optimization process
- Evaluation weights are not orthogonal as mathematicians would say - when you change one weight, you might have to tune others too in response. For example, if you give a higher bonus for having a centralized king, then maybe the material value of the king will drop in response.
- A man is now worth 94 and a king only 105 points (instead of 100 and 130), a much smaller difference than I had programmed originally - as the kings would get more points from other evaluation terms such as centralization than I had given.
- Centralizing men got a negative weight instead of a positive weight as I had originally programmed - putting a man on the squares 10/11/14/15/18/19/22/23 now gets a 3 point penalty instead of a 2 point bonus.
- A red man on 13 that is "in contact" with a white man on 17 gets a bonus of a whopping 29 points instead of the 3-5 points that I had given it at various stages. I'm still surprised at this huge value for such a simple pattern!
How does this compare to AlphaZero?
If you are interested in computers playing games, you must have heard of AlphaZero, Google/Deepmind's innovative way of creating game-playing engines which was originally developed for go, but later also shown to work fine in chess and shogi - doing away with the traditionally used alpha-beta search algorithm, and with the traditional type of evaluation explained above. Instead of an evaluation with features and weights, it uses a very deep neural network (which also includes hundreds of thousands or millions of weights), and instead of the alpha-beta search algorithm it uses something called Monte-Carlo search (MCTS) or variants thereof. In chess, there is an open-source community project called Leela chess zero, based on the ideas used in AlphaZero, which in mid-2019 managed to surpass the dominant traditional engine of the past few years, Stockfish.Switching both the type of evaluation and the type of search was a real paradigm shift for the computer strategy game community, however, it is not clear whether the Monte-Carlo search was really any good. The Stockfish community has since integrated a neural network type of evaluation, but retained the alpha-beta search, and has become the dominant engine once again (much stronger than AlphaZero was). They are using what is called an efficiently updateable neural network or NNUE (spelled out backwards, for some strange reason), and at least for chess, NNUE-type engines seem to be the latest trend. The main point of the NNUE type of neural network is that it runs fast on a normal CPU instead of needing a high-end graphics card like the traditional neural networks.
What Ed did with KingsRow 1.18f, and I finally did with Cake 1.89d is in some ways similar to what AlphaZero was doing - the engines are learning a large part or the whole evaluation by themselves. Our evaluation functions are much simpler than those of AlphaZero, which used a "deep neural network". Both Cake and KingsRow have remained alpha-beta searchers. However, our opening book builders actually have a lot of similarity to the MCTS search used in AlphaZero.
Just recently, Jon Kreuzer published an update of his checkers engine, GuiNN 2.05, which uses an NNUE type evaluation. However, it is currently rather clearly weaker than the machine-learned KingsRow and Cake; but a lot better than our handtuned engines were. I'm not sure why GuiNN is not a lot stronger than our engines with a much simpler evaluation; perhaps the pattern-based approach just works very well for checkers too, as the board and number of pieces are small enough, and the pieces are short-ranged, so that a pattern can encode a lot of knowledge even when looking only at a quarter of the board. This would for example not be the case in chess, where long-range-pieces like bishops, rooks and queens cannot be properly assessed by only looking at 8 squares of the board.
-- Originally written by Martin Fierz on September 18, 2019; last updated June 20th, 2021